Графы
Элементарный минимум
Графы. Применение графов к решению задач
1. Методические рекомендации к теме “Графы”.
Понятие графа целесообразно вводить после того, как разобрано несколько задач, подобных задаче 1, решающее соображение в которых – графическое представление. При обсуждении понятия изоморфизма можно решить несколько упражнений на определение изоморфных и неизоморфных графов. Одно из центральных мест темы – теорема о четности числа нечетных вершин. Чрезвычайно важно также понятие связности графа. Содержательным соображением здесь является рассмотрение компоненты связности, на это необходимо обратить особое внимание. Эйлеровы графы – тема почти игровая.
2. Теоретический материал к теме “Графы”.
Введение
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.
Понятие графа
Рассмотрим две задачи.
Задача 1.Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Решение:Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
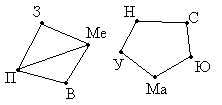
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Задача 2.Доска имеет форму двойного креста, который получается, если из квадрата 4x4 убрать угловые клетки.

Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?
Решение:Занумеруем последовательно клетки доски:
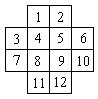
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:
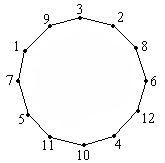
Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.
Такие картинки и называютсяграфами. Точки при этом называютсявершинами, а линии –ребрамиграфа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.
Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:
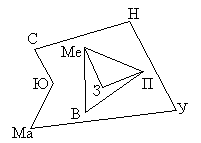
Такие одинаковые, но по-разному нарисованные графы, называютсяизоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.
Задача 3.В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Решение:Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа –5.Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным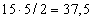 . Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
. Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ.Соединить телефоны таким образом невозможно.
Теорема:Любой граф содержит четное число нечетных вершин.
Доказательство:Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называетсясвязным,если из любые две его вершины можно соединитьпутем,т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.
Задача 4.В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:
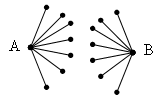
Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны Семерка связен.”
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:
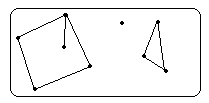
Каждый такой отдельный кусок называетсякомпонентой связности графа.Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:
Задача 5.В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
Доказательство:Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Задача 6.Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?
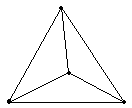
Решение.Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
И в заключение – задача о Кенигсбергских мостах.
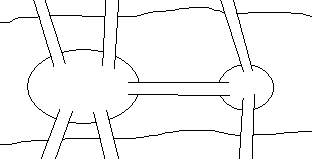
Задача 7.На рисунке изображена схема мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
- На квадратной доске 3x3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?
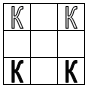 Рис. 1 Рис. 1 |
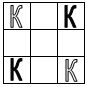 Рис. 2 Рис. 2 |
|---|---|
Решение.Занумеруем клетки доски, как показано на рисунке:
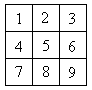
Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:
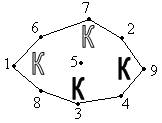 |
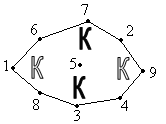 |
|---|---|
При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.
- В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?
Решение.Поставив в соответствие каждому городу точку и соединив точки линией, если сумма цифр делится на 3, получим граф, в котором цифры 3, 5, 9 связаны между собой, но не связаны с остальными. Значит долететь из города 1 в город 9 нельзя.
Степени вершин и подсчет числа ребер.
- В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение.Подсчитаем общее количество выходящих городов дорог – 100.4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.
- В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей ?
Ответ.Нет (теорема о четности числа нечетных вершин).
- У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей ?
Ответ.Нет, не может.
- Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит 100 дорог в таком государстве быть не может.
- Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.
Доказательство непосредственно следует из теоремы о четности числа нечетных вершин графа.
Связность.
- В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.
Доказательство. Рассмотрим компоненту связности, в которую входит один из городов, дорогу между которыми закрыли. По теореме о четности числа нечетных вершин в нее входит и второй город. А значит по-прежнему можно найти маршрут и добраться из одного из этих городов в другой.
Графы Эйлера.
- Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
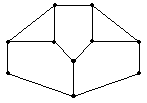
- На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор розно 1 раз?
Продвинутый курс
История возникновения теории графов
Родоначальником теории графов считаетсяЛеонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагаетрешение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.
Терминология теории графов
Терминология теории графов поныне не определена строго. В частности в монографии Гудман, Хидетниеми, 1981 сказано: “В программистском мире нет единого мнения о том, какой из двух терминов"граф"или"сеть". Мы выбрали термин"сеть", так как он, по-видимому, чаще встречается в прикладных областях”. Аналогичная ситуация для “вершина/точка”
Теория графов, Graphentheorie
- в узком смысле - раздел дискретной математики, одна из ветвей дискретной топологии, в широком смысле - теория сетей, наука о топологических формах, сетевых моделях представления любого процесса или системы.. Основным объектом исследования этой теории являются графы. Графом называют геометрическую схему, представляющую собой систему линий, связывающих какие то заданные точки. Точки называемые вершинами, а связывающие их линии - ребрами (или дугами). Теория графов обосновывает способы построения графов, выражающих зависимости или связи в форме геометрических схем между различными единицами той или иной совокупности. Фактически теория графов есть совокупность способов топологических представлений каких-либо процессов или структур.
Многие структуры, представляющие практический интерес в логике, информатике, математике и других науках, могут быть представлены графами. Например, строение любого Интернет ресурса можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки. Вся сеть Интернет - тоже граф. Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Ниже приведены наиболее часто встречаемые определения.
Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.
Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.
Граф в математической теории графов и информатике
- это совокупность непустого множества объектов - вершин и связей между ними. Объекты представляются как вершины, или узлы графа, а связи - как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Неориентированный граф, G-граф
- это упорядоченная пара G := (V, E), для которой выполнены следующие условия:
V - это непустое множество вершин, или узлов,
E - это множество пар (в случае неориентированного графа - неупорядоченных) вершин, называемых рёбрами.
V (а значит и, E, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа.
Порядок графа - это число вершин в графе |V|.
Размер графа - это число его рёбер |E|
Концевые вершины графа
- это вершины, соединяющие данное множество ребер. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть e={v,v}.
Степенью вершины V называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G := (V, A), для которой выполнены следующие условия:
V — это непустое множество вершин или узлов,
A — это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.
Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v \to w ведёт от вершины v к вершине w.
Смешанный G-граф
- это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые - неориентированными. Записывается упорядоченной тройкой G := (V, E, A), где V, E и A определены так же, как выше.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Изоморфный граф
- это некоторый граф G, для которого существует биекция f из множества вершин графа G в множество вершин другого графа H, которому он изоморфен, обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f(A) в вершину f(B) и наоборот - если в графе H есть ребро из вершины A в вершину B, то в графе G должно быть ребро из вершины f^{-1}(A) в вершину f^{-1}(B). В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
Путь графа, цепь графа - это конечная последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированный путь в орграфе - это конечная последовательность вершин v_i (i=1, …,k), для которой все пары (v_i, v_{i+1}) (i=1,… k-1) являются (ориентированными) рёбрами.
Цикл - это путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких “вырожденных” случаев, вводят следующие понятия.
Простой путь (простой цикл) - это такой путь, в котором ребра не повторяются.
Элементарный путь
- это простой путь в графе, вершины в котором не повторяются.
Несложно видеть, что:
Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.
Всякий простой неэлементарный путь содержит элементарный цикл.
Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).
Петля
- это элементарный цикл.
Бинарное отношение на множестве вершин графа, заданное как “существует путь из u в v”, является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. Накомпоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Компонента графа, связная компонента графа
- это всякий максимальный связный подграф G-графа. Слово "максимальный" означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов.
Мост
- это ребро графа, если удаление этого ребра увеличивает число компонент графа.
Связный граф
- это граф, в котором для любых вершин u,v есть путь из u в v.
Сильно связный, ориентированно связный граф
- это ориентированный граф, в котором из любой вершины в любую другую имеется ориентированный путь.
Дерево
- это связный граф, не содержащий простых циклов.
Полный граф
- это граф, в котором любые его две (различные, если не допускаются петли) вершины соединены ребром.
Двудольный граф
- это граф, в котором вершины можно разбить на два непересекающихся подмножества V1 и V2
так, что всякое ребро соединяет вершину из V1 с вершиной из V2.
k-дольный граф
- это граф, в котором вершины можно разбить на k непересекающихся подмножества V_1, V_2, :, V_k так, что не будет рёбер, соединяющих вершины одного и того же подмножества.
Полный двудольный граф
- это граф, в котором каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.
Планарный граф
- это граф, который можно изобразить диаграммой на плоскости без пересечений рёбер.
Взвешенный граф
- это граф, в котором каждому ребру поставлено в соответствие некоторое число, называемое весом ребра.
Существуют также k-раскрашиваемые и k-хроматические графы.
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку (V, E, Ф), где V и E — некоторые множества (вершин и рёбер, соответственно), а Ф — функция инцидентности (или инцидентор), сопоставляющая каждому ребру e<E (упорядоченную или неупорядоченную) пару вершин u и v из V (его концов). Частными случаями этого понятия являются:
- ориентированные графы (орграфы) — когда \varphi(e) всегда является упорядоченной парой вершин;
- неориентированные графы — когда \varphi(e) всегда является неупорядоченной парой вершин;
- смешанные графы — в котором встречаются как ориентированные, так и неориентированные рёбра и петли;
- Эйлеровы графы — граф в котором существует циклический эйлеров путь (Эйлеров цикл).
- мультиграфы — графы с кратными рёбрами, имеющими своими концами одну и ту же пару вершин;
- псевдографы — это мультиграфы, допускающие наличие петель;
- простые графы — не имеющие петель и кратных рёбер.
Под данное выше определение не подходят некоторые другие обобщения:
- гиперграф — если ребро может соединять более двух вершин.
- ультраграф — если между элементами xi и uj существуют бинарные отношения инцидентности.
Объектный граф
- совокупность узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учета взаимных связей в системе, множестве объектов, и не обязательно, чтобы эти связи в точности проецировались в классические связки объектно-ориентированного программирования (такие как отношения старшинства и подчиненности), хотя они моделируют эту парадигму достаточно хорошо. Каждому объекту в объектном графе назначается уникальное числовое значение. Следует иметь в виду, что эти числовые значения, приписываемые членам в объектном графе, произвольны и не имеют никакого смысла вне графа. После назначения всем объектам числового значения объектный граф может начать запись множества зависимостей каждого объекта.
Матрица смежности
- это таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот). Ее недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
Список рёбер
- это тип представления графа, подразумевающий, что каждое ребро представляется двумя числами - номерами вершин этого ребра.
Изображение графов на плоскости
При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.
Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более нагляднуюкартину, чем другие.
Языки описания и программы построения графов
Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых:
- DOT (язык графов)
- GraphML
- Trivial Graph Format
- GML
- GXL
- XGMML
- DGML
Отметим специализированные программы для построения графов. К наиболее удачным относятся коммерческие:
- ILOG
- GoView
- Lassalle AddFlow
- LEDA (есть бесплатная редакция).
Из бесплатных можно отметить Boost Graph Library - Библиотека для работы с графами на языке C++
Для визуализации графов можно использовать:
- Graphviz (по мнению экспертов, она хорошо работает для орграфов)
- LION Graph Visualizer.
- Графоанализатор – это русскоязычная программа, с весьма простым пользовательским интерфейсом.
Некоторые задачи теории графов
Проблема семи мостов Кёнигсберга
- один из первых результатов в теории графов, опубликован Эйлером в 1736.
Проблема четырёх красок
- была сформулирована в 1852 году, но неклассическое доказательство получено лишь в 1976 году (достаточно 4-х красок для карты на сфере (плоскости).
Задача коммивояжёра — одна из наиболее известных NP-полных задач.
Задача о клике — ещё одна NP-полная задача.
Нахождение минимального стягивающего (остовного) дерева.
Изоморфизм графов
- можно ли путем перенумерации вершин одного графа получить другой.
Планарность графа
- можно ли изобразить граф на плоскости без пересечений ребер (или с минимальным числом слоев, что находит применение при трассировке межсоединений элементов печатных плат или микросхем).
К теории графов также относится целый ряд математических проблем, не решенных на сегодняшний день.
Применение теории графов
В химии (для описания структур, путей сложных реакций, правило фаз также может быть интерпретировано как задача теории графов); компьютерная химия — сравнительно молодая область химии, основанная на применении теории графов. Теория графов представляет собой математическую основу хемоинформатики. Теория графов позволяет точно определить число теоретически возможных изомеров у углеводородов и других органических соединений.
В информатике и программировании (граф-схема алгоритма)
В коммуникационных и транспортных системах. В частности, для маршрутизации данных в Интернете.
В схемотехнике (топология межсоединений элементов на печатной плате или микросхеме представляет собой граф или гиперграф).
Литература по теории графов
- Diestel R. Graph Theory, Electronic Edition. - NY: Springer-Verlag, 2005. - С. 422.
- Басакер Р., Саати Т. Конечные графы и сети. М.: Наука, 1974. 368c.
- Белов В. В., Воробьев Е. М., Шаталов В. Е. Теория графов. — М.: Высш. школа, 1976. — С. 392.
- Берж К. Теория графов и ее приложения. М.: ИЛ, 1962. 320c.
- Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И. Лекции по теории графов. М.: Наука, 1990. 384с. (Изд.2, испр. М.: УРСС, 2009. 392 с.)
- Зыков А. А. Основы теории графов. — М.: “Вузовская книга”, 2004. — С. 664. — ISBN 5-9502-0057-8(М.: Наука, 1987. 383c.)
- Кирсанов М. Н. Графы в Maple. - М.: Физматлит, 2007. - 168 c.
- Кристофидес Н.Теория графов. Алгоритмический подход. М.: Мир, 1978. 429c.
- Кормен Т. Х. и др. Часть VI. Алгоритмы для работы с графами // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд.. — М.: Вильямс, 2006. — С. 1296. — ISBN 0-07-013151-1
- Оре О. Теория графов. М.: Наука, 1968. 336с.
- Салий В. Н. Богомолов А. М. Алгебраические основы теории дискретных систем. - М.: Физико-математическая литература, 1997. - ISBN 5-02-015033-9
- Свами М., Тхулалираман К. Графы, сети и алгоритмы. М: Мир, 1984. 455с.
- Татт У. Теория графов. Пер. с англ. М.: Мир, 1988. 424 с.
- Уилсон Р. Введение в теорию графов. Пер с англ. М.: Мир, 1977. 208с.
- Харари Ф. Теория графов. — М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.)
- Харари Ф., Палмер Э. Перечисление графов. — Мир, 1977.
- Уилсон Р. Введение в теорию графов. Пер с англ. М.: Мир, 1977. 208с.
- Харари Ф. Теория графов. М.: Мир, 1973.
- Химические приложения топологии и теории графов. Под ред. Р. Кинга. Пер. с англ. М.: Мир, 1987.