Компьютерные сети
Быстрый расчет IP сетей
В сегодняшней статье мы постараемся отметить основные моменты для быстрого расчета IPv4 сетей. Хоть сейчас и идет постепенный переход на IPv6, все же IPv4 адресация еще долго будет в тренде и умение быстро рассчитывать IPv4 сети многим может пригодиться. Данная статья написана и оформлена совместно с моим коллегой и преподавателем сетевой академии CISCO — Кузьминым Евгением.
Все мы привыкли к отображению IP адреса в виде четырех десятичных чисел, разделенных точками (также их называют октетами, так как они формируются из 8 бит). Все мы знаем, что компьютер для расчетов использует двоичную систему счисления, поэтому для компьютера сетевой адрес, например 192.168.1.1, имеет вид:
11000000 10101000 00000001 00000001
Маска подсети в двоичном виде выглядит как последовательность единиц, а затем нулей и указывает на то, сколько первых битов IP-адреса будут относится к адресу сети (у всех компьютеров в одной сети они будут одинаковые), а остальные биты будут относится к адресу каждого узла (у всех компьютеров в одной сети они будут разные). Есть специальные адреса: адрес сети — адрес, у которого узловая часть состоит из одних нулей, и широковещательный адрес — это адрес, у которого узловая часть состоит из одних единиц. Например, маска вида 255.255.255.0 в двоичном виде выглядит:
11111111 11111111 111111111 00000000
и указывает на то, что первые 24 бита относятся к адресу сети, а последние восемь к адресу конкретного узла в этой сети. Маска сети также может быть записана, как просто число, указывающее количество первых битов, относящихся к адресу сети. В данном случае — 24.
Со стандартными маскам все легко, они имеют вид; 255.0.0.0, 255.255.0.0 и 255.255.255.0 и четко отделяют узловую часть от сетевой по границе каждого октета. Поэтому, для формировани адреса сети, октеты, у которых маска 255, мы не изменяем. а октеты у которых маска 0, превращаем в 0 (для широковещательного адреса в 255). Напимер, для адреса 192.168.25.128 с маской 255.255.0.0, адрес сети будет 192.168.0.0, а широковещательный – 192.168.255.255.
Но когда нужно разделить сети на более мелкие подсети или объединить несколько сетей в одну общую могут возникнуть сложности. Основное — это запомнить, что каждое десятичное число в адресе состоит из 8 двоичных битов, и нужно знать десятичное значение каждого бита, которое является степенью двойки.

Любое число в адресе является суммой некоторых степеней двойки. Чтобы определить каких, нужно их последовательно складывать, двигаясь от 128 к 1, если сумма будет превышать нужное число, то эту степень пропускаем. Ниже приведу несколько примеров, в которых покажу основные алгоритмы расчета.
Пример 1
Есть IP адрес 192.168.1.37/28, необходимо определить адрес сети и широковещательный адрес.
- Всего бит в адресе: 32, количество бит на адрес сети: 28, следовательно количество бит на адреса узлов: 32 – 28 = 4 бита.
- Количество возможных адресов для подсети: 2^4 = 16.
- Количество адресов для хостов (за минусом адреса сети и широковещательного адреса): 16 – 2 = 14.
- У адреса сети значения первых трех октетов будет таким же, как у адреса хоста, а значение последнего октета будет наибольшее число, не превышающее его значения в адресе хоста, кратное 16. И следовательно может формироваться из суммы: 128 или 64 или 32 или 16.
- Получаем адрес сети: 192.168.1.32
- Широковещательный адрес получаем прибавив к последнему октету адреса сети количество адресов сети минус 1: 192.168.1.{32+16-1}= 192.168.1.47
Пример 2
Есть IP адрес 192.168.1.37/255.255.255.240, необходимо определить адрес сети.
- Количество адресов для подсети можно получить: 256 — 240 = 16.
- Количество адресов для хостов 16 – 2 = 14.
- У адреса сети, как и в прошлом примере, значения первых трех октетов будет таким же, как у адреса хоста, а значение последнего октета будет наибольшее число, не превышающее его значения в адресе хоста, кратное 16. И следовательно может формироваться из суммы: 128 или 64 или 32 или 16.
Получаем адрес сети 192.168.1.32
Пример 3
Записать маску вида 255.255.255.240 в маску вида “/x”.
- 256 – 240 = 16.
- 16 = 2^4. 4 бита отводятся на адреса.
- А так как всего бит 32, то 32 – 4 = 28.
Значит 255.255.255.240 = /28
Пример 4
Записать маску вида /28 в маску вида XXX.XXX.XXX.XXX
- Всего бит: 32.
- Количество Бит на адреса: 32 – 28 = 4.
- 2^4=16. 16 адресов в подсети.
- 256 – 16 = 240.
Значит маска: 255.255.255.240.
Дополнительный материал
Перевод чисел в различные системы счислений
Когда занимаешься настройками сетей различного масштаба и каждый день сталкиваешься с вычислениями – то такого рода шпаргалки заводить не обязательно, все и так делается на безусловном рефлексе. Но когда в сетях ковыряешься очень редко, то не всегда вспомнишь какая там маска в десятичной форме для префикса 21 или же какой адрес сети при этом же префиксе. В связи с этим я и решил написать несколько маленьких статей-шпаргалок по переводом чисел в различные системы счислений, сетевым адресам, маскам и т.п. В это части пойдет речь о переводи чисел в различные системы счислений.
1. Системы счислений
Когда вы занимаетесь чем-то связанным с компьютерными сетями и ИТ, вы по любому столкнетесь с этим понятием. И как толковый ИТ-шник вам нужно разбираться в этом хотя бы чу-чуть даже если на практике вы это будете применять очень редко.
Рассмотрим перевод каждой цифры из IP-адреса98.251.16.138в следующие системы счислений:
- Двоичная
- Восьмеричная
- Десятичная
- Шестнадцатеричная
1.1 Десятичная
Так как цифры записаны в десятичной, перевод с десятичной в десятичную пропустим 🙂
1.1.1 Десятичная → Двоичная
Как мы знаем двоичная система счисления используется практически во всех современных компьютерах и многих других вычислительных устройствах. Система очень проста – у нас есть только 0 и 1.
Для преобразования числа с десятиной в двоичную форму нужно использовать деление по модулю 2 (т.е. целочисленное деление на 2) в результате чего мы всегда будем иметь в остатке либо 1, либо 0. При этом результат записываем справа налево. Пример все поставит на свои места:
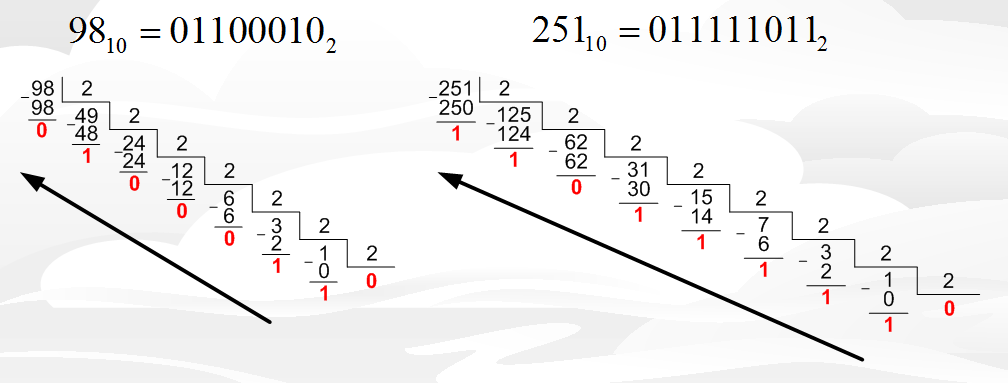
Рисунок 1.1 – Перевод чисел из десятичной в двоичную систему
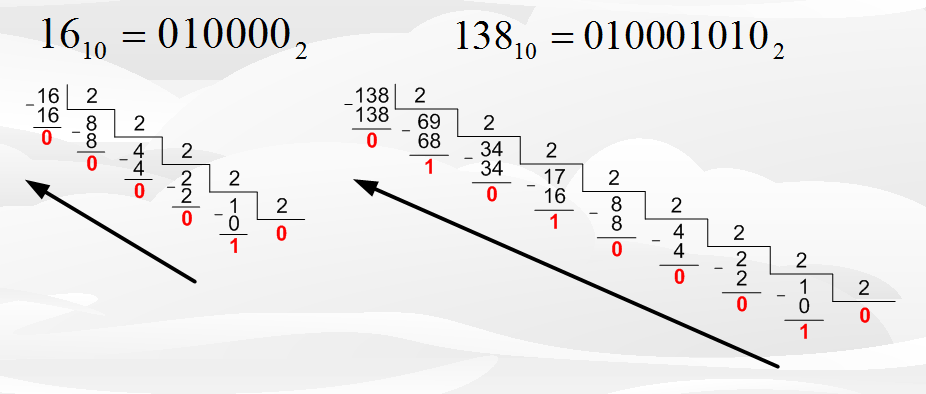
Рисунок 1.2 – Перевод чисел из десятичной в двоичную систему
Опишу деление числа 98. Мы делим 98 на 2, в результате имеем 49 и остаток 0. Далее продолжаем деление и делим 49 на 2, в результате имеем 24 с остатком 1. И таким же образом добираемся до 1-ки или 0-ка в делимом. Затем результат записываем справа налево.
1.1.2 Десятичная → Восьмеричная
Восьмеричная система – это целочисленная система счисления с основанием 8. Т.е. все числа в ней представлены диапазоном 0 – 7 и для перевода с десятичной системы нужно использовать деление по модулю 8.
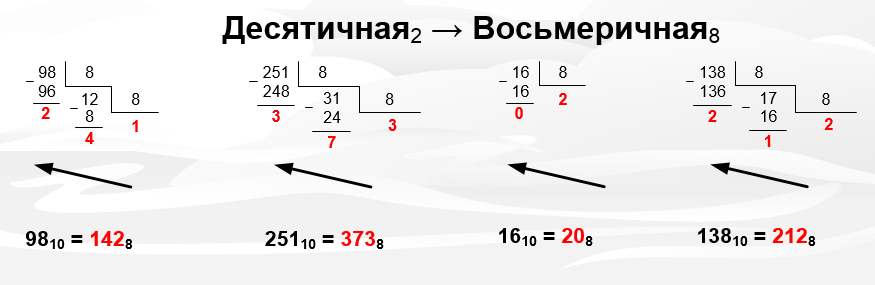
Рисунок 1.3 – Перевод чисел из десятичной в восьмеричную систему
Деление аналогично 2-чной системе.
1.1.3 Десятичная → Шестнадцатеричная
Шестнадцатеричная система почти полностью вытеснила восьмеричную систему. У нее основание 16, но используются десятичные цифры от 0 до 9 + латинские буквы от A(число 10) до F(число 15). С ней вы сталкиваетесь каждый раз, когда проверяете настройки сетевого адаптера — это МАС-адрес. Так же, когда используется IPv6.
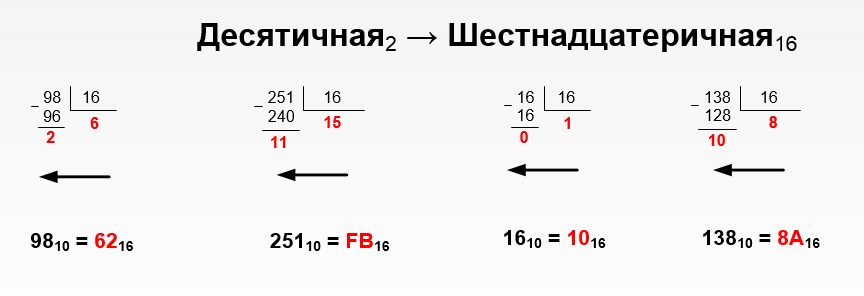
Рисунок 1.4 – Перевод чисел из десятичной в шестнадцатеричную систему
1.2 Двоичная
В предыдущем примере мы перевели все десятичные числа в другие системы счислений, одна из которых двоичная. Теперь переведем каждое число с двоичной формы.
1.2.1 Двоичная → Десятичная
Для перевода чисел с двоичной формы в десятичную нужно знать два нюанса. Первый – у каждого нолика и единички есть множитель 2 в n-й степени, при котором n увеличивается справа налево ровно на единичку. Второй – после перемножения все числа нужно сложить и мы получим число в десятичной форме. В итого у нас будет формула такого вида:
D = (an× pn-1) + (an-1× pn-2) + (an-2× pn-3) +…, (1.2.1)
Где,
D – это число в десятичной форме, которое мы ищем;
n– количество символов в двоичном числе;
a – число в двоичной форме на n-й позиции (т.е. первый символ, второй, и т.п.);
p – коэффициент, равный 2,8 или 16 в степениn(в зависимости от системы счисления)
К примеру возьмем число 110102. Смотрим на формулу и записываем:
- Число состоит из 5 символов ( n =5)
a5= 1, a4= 1, a3= 0, a2= 1, a1= 0
p = 2 (так как переводим из двоичной в десятичную)
В итоге имеем:
D = (1 × 25-1) + (1 × 25-2) + (0 × 25-3) + (1 × 25-4) + (0 × 25-5) = 16 + 8 + 0 + 2 + 0 = 2610
Кто привык записывать справа на лево, форму будет выглядеть так:
D = (0 × 25-5) + (1 × 25-4) + (0 × 25-3) + (1 × 25-2) + (1 × 25-1) = 0 + 2 + 0 + 8 + 16 = 2610
Но, как мы знаем, от перестановки слагаемых сумма не меняется. Давайте теперь переведем наши числа в десятичную форму.

Рисунок 1.5 – Перевод чисел из двоичной в десятичную систему
1.2.2 Двоичная → Восьмеричная
При переводе нам нужно двоичное число разбить на группы по три символа справа налево. Если последняя группа не состоит из трех символов, то мы просто возмещаем недостающие биты ноликами. К примеру:
10101001 =010 101 001
1011100 =001 011 100
Каждая группа битов – это одно из восьмеричных чисел. Чтобы узнать какое, нужно использовать написанную выше формулу 1.2.1 для каждой группы битов. В результате мы получим.

Рисунок 1.6 – Перевод чисел из двоичной в восьмеричную систему
1.2.3 Двоичная → Шестнадцатеричная
Здесь нам нужно двоичное число разбивать на группы по четыре символа справа налево с последующим дополнением недостающих битов группы ноликами, как писалось выше. Если последняя группа состоит из ноликов, то их нужно игнорировать.
110101011 =0001 1010 1011
1011100 =0101 1100
001010000 =000101 0000 = 0101 0000
Каждая группа битов – это одно из шестнадцатеричных чисел. Используем формулу 1.2.1 для каждой группы битов.

Рисунок 1.7 – Перевод чисел из двоичной в шестнадцатеричную систему
1.3 Восьмеричная
В этой системе у нас могут возникнуть сложности только при переводе в 16-ричную систему, так как остальной перевод проходит гладко.
1.3.1 Восьмеричная → Двоичная
Каждое число в восьмеричной системе – это группа из трех битов в двоичной системе, как писалось выше. Для перевода нам нужно воспользоваться табличкой-шпаргалкой:

Рисунок 1.8 – Шпора по переводу чисел из восьмеричной системы
Используя эту табличку переведем наши числа в двоичную систему.
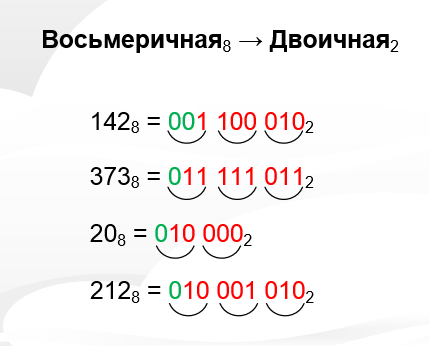
Рисунок 1.9 – Перевод чисел из восьмеричной в двоичную систему
Немного опишу вывод. Первое число у нас 142, значит будет три группы по три бита в каждой. Юзаем шпору и видим, что цифра 1 это 001, цифра 4 это 100 и цифра 2 это 010. В результате имеем число 001100010.
1.3.2 Восьмеричная → Десятичная
Здесь мы используем формулу 1.2.1 только с коэффициентом 8 (т.е. p=8). В результате имеем

Рисунок 1.10 – Перевод чисел из восьмеричной в десятеричную систему
Возьмем первое число. Исходя из формулы 1.2.1:
- Число состоит из 3 символов ( n =3)
a3= 1, a2= 4, a1= 2
p = 8 (так как переводим из восьмеричной в десятичную)
В результате имеем:
D = (1 × 83-1) + (4 × 83-2) + (2 × 83-3) = 64 + 32 + 2 = 9810
1.3.3 Восьмеричная → Шестнадцатеричная
Как писалось раньше, для перевода нам нужно сначала перевести числа в двоичную систему, потом с двоичной в шестнадцатеричную, поделив на группы по 4-ре бита. Можно использовать следующею шпору.

Рисунок 1.11 – Шпора по переводу чисел из шестнадцатеричной системы
Эта табличка поможет перевести из двоичной в шестнадцатеричную систему. Теперь переведем наши числа.

Рисунок 1.12 – Перевод чисел из восьмеричной в шестнадцатеричную систему
1.4 Шестнадцатеричная
В этой системе та же проблема, при переводе в восьмеричную. Но об этом позже.
1.4.1 Шестнадцатеричная → Двоичная
Каждое число в шестнадцатеричной системе – это группа из четырех битов в двоичной системе, как писалось выше. Для перевода нам можно воспользоваться табличкой-шпаргалкой, которая находиться выше. В результате:

Рисунок 1.13 – Перевод чисел из шестнадцатеричной в двоичную систему
Возьмем первое число – 62. Используя табличку (рис. 1.11) мы видим, что 6 это 0110, 2 это 0010, в результате имеем число 01100010.
1.4.2 Шестнадцатеричная → Десятичная
Здесь мы используем формулу 1.2.1 только с коэффициентом 16 (т.е. p=16). В результате имеем

Рисунок 1.14 – Перевод чисел из шестнадцатеричной в десятеричную систему
Возьмем первое число. Исходя из формулы 1.2.1:
- Число состоит из 2 символов ( n =2)
a2= 6, a1= 2
p = 16 (так как переводим из шестнадцатеричной в десятичную)
В результате имеем.
D = (6 × 162-1) + (2 × 162-2) = 96 + 2 = 9810
1.4.3 Шестнадцатеричная → Восьмеричная
Для перевода в восьмеричную систему нужно сначала перевести в двоичную, затем разбить на группы по 3-и бита и воспользоваться табличкой (рис. 1.8). В результате:

Рисунок 1.15 – Перевод чисел из шестнадцатеричной в восьмеричную систему
Классы IP адресов и планирование сетей
Умение переводить числа в различные системы счислений поможет нам разделять сетевую и хостовую части для различного масштаба сетей, определять максимальное количество устройств(хостов) в сети, определять адрес сети и широковещательный адрес, и т.п. Об этом всем и пойдет речь в данной статье. Так как мы будем обсуждать и работать с IPv4 адресами – начнем с теории и потом плавно перейдем к практике.
1. IP-адреса
IP-адрес – это число, которое позволяет (должно) уникально идентифицировать узел компьютерной сети. Одним словом – это идентификатор с которым вы можете лазить по сетям и обмениваться информацией с различными сервисами и устройствами. Адрес представляет собой четыре октета (8 двоичных разрядов) разделенных точкой – общая длинна 32 бита.
Сам по себе IP-адрес состоит из сетевой и хостовой частей, по которой определяется номер сети и номер узла. Для определения этих параметров используется два вида адресации:
- Классовая
- Бесклассовая
1.1 Классовая адресация
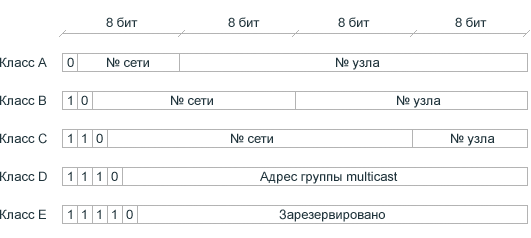
Сначала все сети строились используя только этого вид адресации, поскольку никто не думал, что пул адресов так быстро иссякнет. Здесь номер сети и узла определялись используя классы, в которых по первым битам можно было определить номер сети, а все остальное отводилось на узел (рис. 1.1.1).
Рисунок 1.1.1 – Распределение битов в классовой адресации
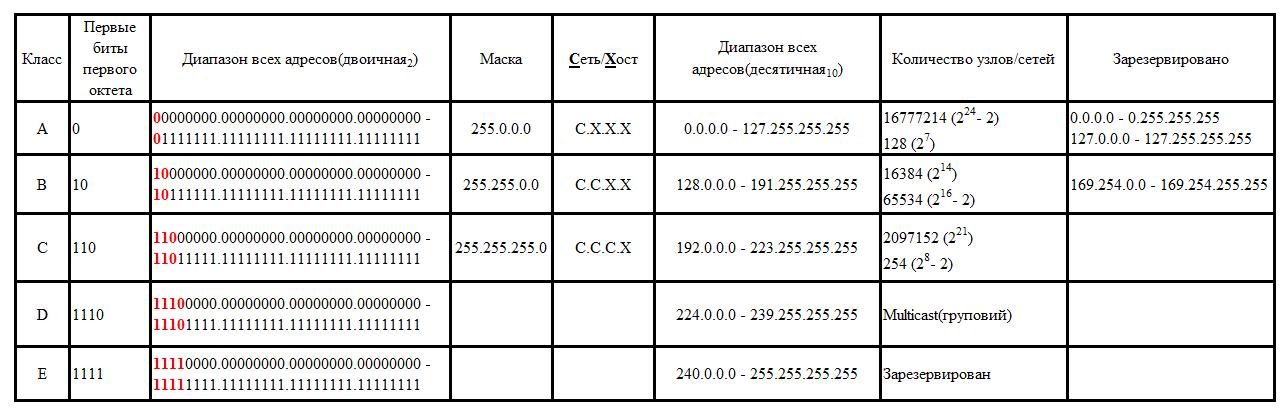
В классовой адресации все сети делились на 5 классов. Каждый класс имеет свой диапазон адресов, но не все адреса из данного диапазона можно использовать. Многие из них зарезервированы (рис. 1.1.2).
Рисунок 1.1.2 – Особенности классовой адресации
С этой таблицы можно увидеть диапазоны адресов каждого из классов, маску сетей для каждого класса, доступное количество хостов и сетей и диапазон некоторых зарезервированных адресов по каждому из классов (список всех зарезервированных адресов можно найти вrfc3330).
Каждый из А, В, С классов сетей имеет диапазон адресов, которые используются в локальных сетях и относятся к частным (private). Вот эти диапазоны:
10.0.0.0/8 10.0.0.0 — 10.255.255.255
172.16.0.0/12 172.16.00 — 172.31.255.255
192.168.0.0/16 192.168.0.0 — 192.168.255.255
Любой из этих диапазонов можно использовать в локальных сетях, но если использовать классовую адресацию, то минимальное количество узлов в сети может быть – 254, если брать класс С. И когда у нас ситуация, что нужно в одной сети иметь, к примеру, 500 компьютеров, то нужно уже резервировать класс В, и брать маску 16 с 65534 доступными IP – чего нам вообще не нужно. В связи з этим (и не только этим), и стали переходить на бесклассовою адресацию.
1.2 Бесклассовая адресация
Данный вид адресации еще называют CIDR (Classless Inter-Domain Routing). В отличии от классовой (длинна маски фиксирована по октетам), здесь можно сэкономить IP-адреса используя маски переменной длинны (VLSM — variable length subnet mask). В этом случаи на 500 компьютеров можно резервировать любой класс сети (А, В, С), но с маской – 255.255.254.0 (префикс — /23). Диапазон адресов будет следующим:
10.0.0.0 – 10.0.1.255
172.16.0.0 – 172.16.1.255
192.168.0.0 – 192.168.1.255
В каждом из диапазонов у нас будет 510 хостов. О том, как это подсчитать пойдет речь в следующей главе.
1.3 Планирование сети
После того, как мы немного познакомились с сетями, пора переходить к практике. При планировании сети предприятия нужно в первую очередь определиться с классом сети и возможным количеством конечных узлов сети (компьютеров, сетевых принтеров, wi-fi роутеров, телефонов, ноутбуков, виртуальных машин, и т.п.). Класс не столько важен, сколько максимальное количество хостов, которое определяется по формуле:
Х = 2n— 2, (1.3.1)
Где,
Х – это количество хостов в подсети;
n – количество бит отведенных на хостовую часть;
Мы отнимаем 2, потому что в каждой из сетей резервируется два адреса:
- Адрес сети (все биты отведенные на хостовую часть равны нулю)
- Широковещательный адрес (все биты отведенные на хостовую часть равны единице)
Каждую сеть можно разбить на подсети. Количество подсетей считается по формуле:
С = 2n, (1.3.2)
Где,
С – это количество подсетей;
n – количество бит отведенных на адрес сети;
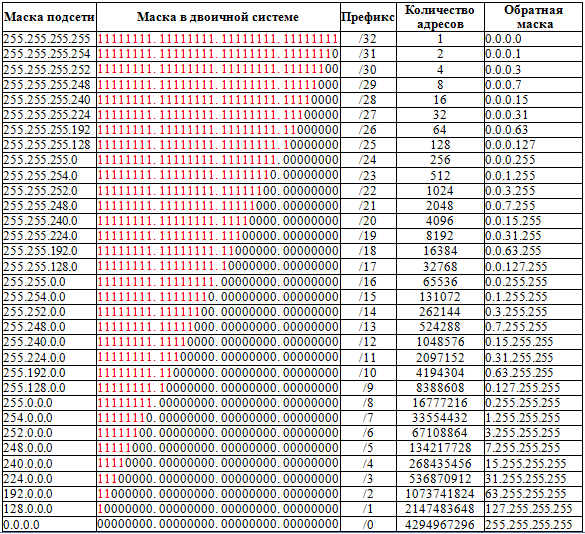
Еще, при расчете, нам понадобится заранее подготовленная таблица с масками сетей в двоичной и, соответственно, десятичной форме и указанием максимального количества хостов в сети (рис. 1.3.1).
Рисунок 1.3.1 – Маски подсетей в десятичной и двоичной форме с соответствующим префиксом и максимальным количеством хостов
Давайте помечтаем, что у нас огромное предприятие с 250000 хостами, которые должны получить уникальный IP-адрес. Используя рис. 1.3.1 видим, что для этого нам нужна маска 255.252.0.0, которая покроет чуть больше 250 000 адресов. Префикс сети равен 14. Префикс – это краткое обозначение количества единичек в сетевой части.
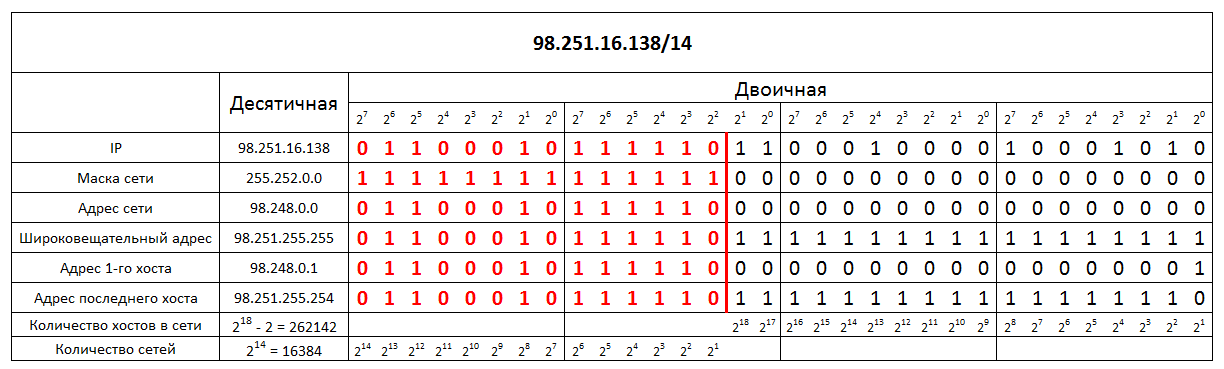
Теперь возьмем, к примеру, IP-адрес спредыдущей статьис префиксом 14 (98.251.16.138/14) и на его базе определим:
- Адрес сети
- Широковещательный адрес
- Адрес первого хоста сети
- Адрес последнего хоста сети
- Максимальное количество хостов в сети
- Количество сетей
Рисунок 1.3.2 – Подсчет параметров сети
Теперь объясню, что здесь было сделано. Для начала мы перевели каждый октет из десятичной формы в двоичную и провели грань между адресом сети и хостовой частью используя маску. В результате получили адрес сети (красное) и хостовую часть в двоичной форме. Теперь нужно перевести адрес сети в десятичную форму, для этого пользуемсяпредыдущей статьейи у нас получается адрес – 98.248.0.0. Теперь таким же образом узнаем широковещательный адрес (где вся хостовая часть равна единичкам) и получаем – 98.251.255.255. Оба этих адреса мы не можем использовать как адреса хоста, так как они зарезервированы уже. Теперь первый адрес хоста – это адрес сети плюс единичка (т.е. 98.248.0.1), а последний – это широковещательный адрес минус единичка (т.е. 98.251.255.254). Количество сетей и хостов определяем по формуле 1.3.1 и 1.3.2.
Вот и все.