Системы счисления
Внимание!
Для решения задач ГИА - 9 достаточно знать и понимать как кодируется информация в двоичном счислении. Знания о 8-ричной и 16-ричной системах желательны, но не обязательны!
Для начала надо запомнить
1) Отсчет начинается не с 1, как привыкли в первом классе, а с 0
2) Название счисления "Десятичная", "Двоичная", "Восьмеричная", "Шестнадцатеричная" - обозначает то, что следующий разряда начинается с числа по названию которого обозначена система. Других чисел для продолжения ряда цифр просто нет.
Сложность для восприятия представляет шестнадцатиричная система, в которой после 15 следуют цифры обозначаемые буквами от "А" до "F".
Важно помнить, что следующий кратный разряд обозначается степенью числа разряда кратного 10.
Таблица систем счисления
| Десятичная А10 | Двоичная А2 | Восьмеричная А8 | Шестнадцатиричная А16 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |
| 20 | 10100 | 24 | 14 |
| 21 | 10101 | 25 | 15 |
| 22 | 10110 | 26 | 16 |
| 23 | 10111 | 27 | 17 |
| 24 | 11000 | 30 | 18 |
| 25 | 11001 | 31 | 19 |
| 26 | 11010 | 32 | 1A |
| 27 | 11011 | 33 | 1B |
| 28 | 11100 | 34 | 1C |
Пресчёт систем счисления между собой
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
 |
1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Пример .Число перевести в десятичную систему счисления.
перевести в десятичную систему счисления.

2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
 |
1 | 8 | 64 | 512 | 4096 | 32768 | 262144 |
Пример .Число перевести в десятичную систему счисления.
перевести в десятичную систему счисления.

3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
 |
1 | 16 | 256 | 4096 | 65536 | 1048576 | 16777216 |
Пример .Число перевести в десятичную систему счисления.
перевести в десятичную систему счисления.

4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример.Число перевести в двоичную систему счисления.
перевести в двоичную систему счисления.


5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример.Число перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.


6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример.Число перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.


7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример.Число перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.

8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример.Число перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.

9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример.Число перевести в двоичную систему счисления.
перевести в двоичную систему счисления.

10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример.Число перевести в двоичную систему счисления.
перевести в двоичную систему счисления.

11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1.Число перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.

Пример 2.Число перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.

Дополнительный материал
Перевод чисел в различные системы счислений
Когда занимаешься настройками сетей различного масштаба и каждый день сталкиваешься с вычислениями – то такого рода шпаргалки заводить не обязательно, все и так делается на безусловном рефлексе. Но когда в сетях ковыряешься очень редко, то не всегда вспомнишь какая там маска в десятичной форме для префикса 21 или же какой адрес сети при этом же префиксе. В связи с этим я и решил написать несколько маленьких статей-шпаргалок по переводом чисел в различные системы счислений, сетевым адресам, маскам и т.п. В это части пойдет речь о переводе чисел в различные системы счислений.
1. Системы счислений
Когда вы занимаетесь чем-то связанным с компьютерными сетями и ИТ, вы по любому столкнетесь с этим понятием. И как толковый ИТ-шник вам нужно разбираться в этом хотя бы чу-чуть даже если на практике вы это будете применять очень редко.
Рассмотрим перевод каждой цифры из IP-адреса98.251.16.138в следующие системы счислений:
- Двоичная
- Восьмеричная
- Десятичная
- Шестнадцатеричная
1.1 Десятичная
Так как цифры записаны в десятичной, перевод с десятичной в десятичную пропустим 🙂
1.1.1 Десятичная → Двоичная
Как мы знаем двоичная система счисления используется практически во всех современных компьютерах и многих других вычислительных устройствах. Система очень проста – у нас есть только 0 и 1.
Для преобразования числа с десятиной в двоичную форму нужно использовать деление по модулю 2 (т.е. целочисленное деление на 2) в результате чего мы всегда будем иметь в остатке либо 1, либо 0. При этом результат записываем справа налево. Пример все поставит на свои места:
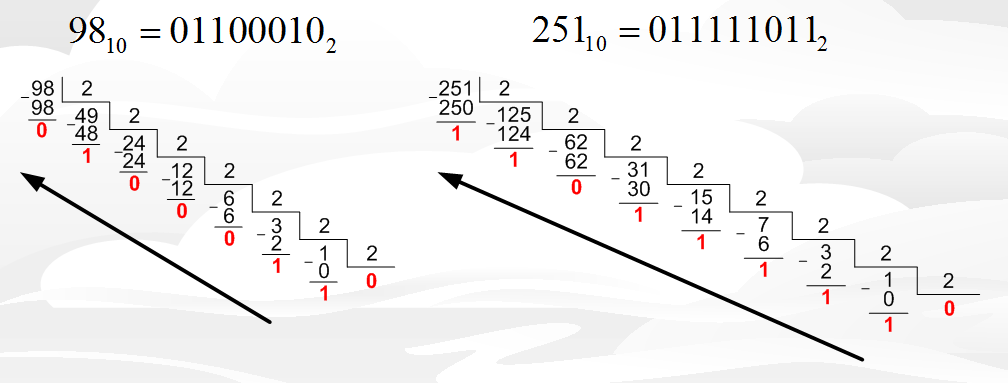
Рисунок 1.1 – Перевод чисел из десятичной в двоичную систему
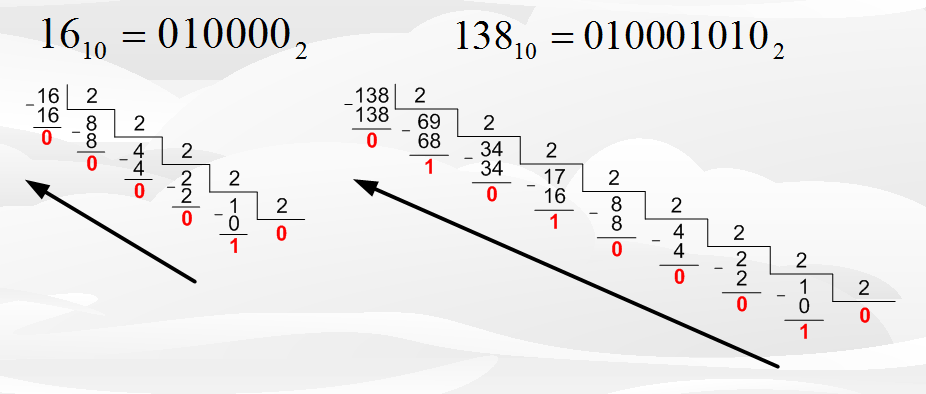
Рисунок 1.2 – Перевод чисел из десятичной в двоичную систему
Опишу деление числа 98. Мы делим 98 на 2, в результате имеем 49 и остаток 0. Далее продолжаем деление и делим 49 на 2, в результате имеем 24 с остатком 1. И таким же образом добираемся до 1-ки или 0-ка в делимом. Затем результат записываем справа налево.
1.1.2 Десятичная → Восьмеричная
Восьмеричная система – это целочисленная система счисления с основанием 8. Т.е. все числа в ней представлены диапазоном 0 – 7 и для перевода с десятичной системы нужно использовать деление по модулю 8.
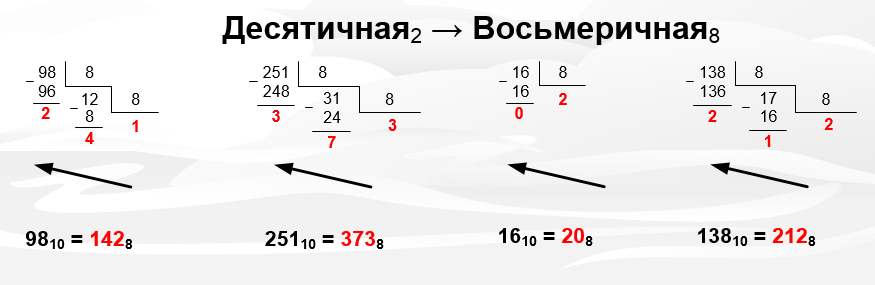
Рисунок 1.3 – Перевод чисел из десятичной в восьмеричную систему
Деление аналогично 2-чной системе.
1.1.3 Десятичная → Шестнадцатеричная
Шестнадцатеричная система почти полностью вытеснила восьмеричную систему. У нее основание 16, но используются десятичные цифры от 0 до 9 + латинские буквы от A(число 10) до F(число 15). С ней вы сталкиваетесь каждый раз, когда проверяете настройки сетевого адаптера — это МАС-адрес. Так же, когда используется IPv6.
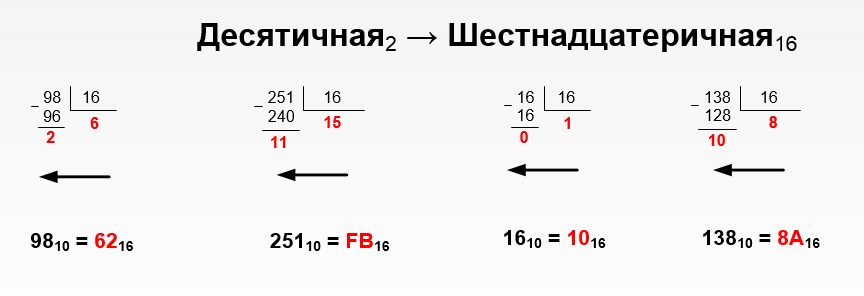
Рисунок 1.4 – Перевод чисел из десятичной в шестнадцатеричную систему
1.2 Двоичная
В предыдущем примере мы перевели все десятичные числа в другие системы счислений, одна из которых двоичная. Теперь переведем каждое число с двоичной формы.
1.2.1 Двоичная → Десятичная
Для перевода чисел с двоичной формы в десятичную нужно знать два нюанса. Первый – у каждого нолика и единички есть множитель 2 в n-й степени, при котором n увеличивается справа налево ровно на единичку. Второй – после перемножения все числа нужно сложить и мы получим число в десятичной форме. В итого у нас будет формула такого вида:
D = (an× pn-1) + (an-1× pn-2) + (an-2× pn-3) +…, (1.2.1)
Где,
D – это число в десятичной форме, которое мы ищем;
n– количество символов в двоичном числе;
a – число в двоичной форме на n-й позиции (т.е. первый символ, второй, и т.п.);
p – коэффициент, равный 2,8 или 16 в степениn(в зависимости от системы счисления)
К примеру возьмем число 110102. Смотрим на формулу и записываем:
- Число состоит из 5 символов ( n =5)
a5= 1, a4= 1, a3= 0, a2= 1, a1= 0
p = 2 (так как переводим из двоичной в десятичную)
В итоге имеем:
D = (1 × 25-1) + (1 × 25-2) + (0 × 25-3) + (1 × 25-4) + (0 × 25-5) = 16 + 8 + 0 + 2 + 0 = 2610
Кто привык записывать справа на лево, форму будет выглядеть так:
D = (0 × 25-5) + (1 × 25-4) + (0 × 25-3) + (1 × 25-2) + (1 × 25-1) = 0 + 2 + 0 + 8 + 16 = 2610
Но, как мы знаем, от перестановки слагаемых сумма не меняется. Давайте теперь переведем наши числа в десятичную форму.

Рисунок 1.5 – Перевод чисел из двоичной в десятичную систему
1.2.2 Двоичная → Восьмеричная
При переводе нам нужно двоичное число разбить на группы по три символа справа налево. Если последняя группа не состоит из трех символов, то мы просто возмещаем недостающие биты ноликами. К примеру:
10101001 =010 101 001
1011100 =001 011 100
Каждая группа битов – это одно из восьмеричных чисел. Чтобы узнать какое, нужно использовать написанную выше формулу 1.2.1 для каждой группы битов. В результате мы получим.

Рисунок 1.6 – Перевод чисел из двоичной в восьмеричную систему
1.2.3 Двоичная → Шестнадцатеричная
Здесь нам нужно двоичное число разбивать на группы по четыре символа справа налево с последующим дополнением недостающих битов группы ноликами, как писалось выше. Если последняя группа состоит из ноликов, то их нужно игнорировать.
110101011 =0001 1010 1011
1011100 =0101 1100
001010000 =000101 0000 = 0101 0000
Каждая группа битов – это одно из шестнадцатеричных чисел. Используем формулу 1.2.1 для каждой группы битов.

Рисунок 1.7 – Перевод чисел из двоичной в шестнадцатеричную систему
1.3 Восьмеричная
В этой системе у нас могут возникнуть сложности только при переводе в 16-ричную систему, так как остальной перевод проходит гладко.
1.3.1 Восьмеричная → Двоичная
Каждое число в восьмеричной системе – это группа из трех битов в двоичной системе, как писалось выше. Для перевода нам нужно воспользоваться табличкой-шпаргалкой:

Рисунок 1.8 – Шпора по переводу чисел из восьмеричной системы
Используя эту табличку переведем наши числа в двоичную систему.
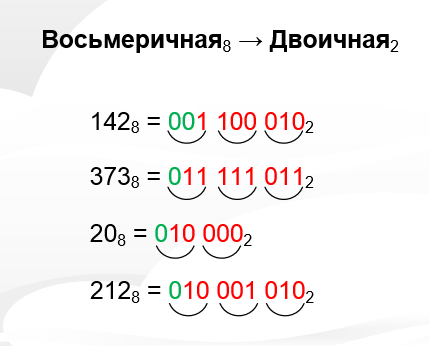
Рисунок 1.9 – Перевод чисел из восьмеричной в двоичную систему
Немного опишу вывод. Первое число у нас 142, значит будет три группы по три бита в каждой. Юзаем шпору и видим, что цифра 1 это 001, цифра 4 это 100 и цифра 2 это 010. В результате имеем число 001100010.
1.3.2 Восьмеричная → Десятичная
Здесь мы используем формулу 1.2.1 только с коэффициентом 8 (т.е. p=8). В результате имеем

Рисунок 1.10 – Перевод чисел из восьмеричной в десятеричную систему
Возьмем первое число. Исходя из формулы 1.2.1:
- Число состоит из 3 символов ( n =3)
a3= 1, a2= 4, a1= 2
p = 8 (так как переводим из восьмеричной в десятичную)
В результате имеем:
D = (1 × 83-1) + (4 × 83-2) + (2 × 83-3) = 64 + 32 + 2 = 9810
1.3.3 Восьмеричная → Шестнадцатеричная
Как писалось раньше, для перевода нам нужно сначала перевести числа в двоичную систему, потом с двоичной в шестнадцатеричную, поделив на группы по 4-ре бита. Можно использовать следующею шпору.

Рисунок 1.11 – Шпора по переводу чисел из шестнадцатеричной системы
Эта табличка поможет перевести из двоичной в шестнадцатеричную систему. Теперь переведем наши числа.

Рисунок 1.12 – Перевод чисел из восьмеричной в шестнадцатеричную систему
1.4 Шестнадцатеричная
В этой системе та же проблема, при переводе в восьмеричную. Но об этом позже.
1.4.1 Шестнадцатеричная → Двоичная
Каждое число в шестнадцатеричной системе – это группа из четырех битов в двоичной системе, как писалось выше. Для перевода нам можно воспользоваться табличкой-шпаргалкой, которая находиться выше. В результате:

Рисунок 1.13 – Перевод чисел из шестнадцатеричной в двоичную систему
Возьмем первое число – 62. Используя табличку (рис. 1.11) мы видим, что 6 это 0110, 2 это 0010, в результате имеем число 01100010.
1.4.2 Шестнадцатеричная → Десятичная
Здесь мы используем формулу 1.2.1 только с коэффициентом 16 (т.е. p=16). В результате имеем

Рисунок 1.14 – Перевод чисел из шестнадцатеричной в десятеричную систему
Возьмем первое число. Исходя из формулы 1.2.1:
- Число состоит из 2 символов ( n =2)
a2= 6, a1= 2
p = 16 (так как переводим из шестнадцатеричной в десятичную)
В результате имеем.
D = (6 × 162-1) + (2 × 162-2) = 96 + 2 = 9810
1.4.3 Шестнадцатеричная → Восьмеричная
Для перевода в восьмеричную систему нужно сначала перевести в двоичную, затем разбить на группы по 3-и бита и воспользоваться табличкой (рис. 1.8). В результате:

Рисунок 1.15 – Перевод чисел из шестнадцатеричной в восьмеричную систему
Система Горнера
Основные понятия систем счисления
Системой счисленияилинумерациейназывается определенный способ записи чисел. Из Базового курса информатики вы знакомы с историей систем счисления, знаете, что системы счисления бывают позиционными и непозиционными. Вам также известно, что привычная для нас система счисления называется десятичной позиционной системой, что в компьютере для представления чисел и выполнения вычислений используется двоичная система счисления.
Числа заключают в себе количественную информацию. Запись чисел по правилам определенной системы счисления естьспособ кодирования чисел. От способа кодирования зависит размер кода, т.е. количество цифр в записи числа, а также правила выполнения вычислений. Одной из главных проблем, которую нужно было решить изобретателям ЭВМ, это проблема представления чисел в памяти компьютера и алгоритма их обработки (вычислений) процессором. Для понимания того, как были решены эти проблемы нужно знать принципы организации систем счисления.
Основные понятия позиционных систем счисления
Цифра– символ, используемый для записи чисел.
Алфавитсистемы счисления – совокупность всех цифр.
Размерность алфавита– количество цифр в алфавите.
В записи многозначного числа цифры, стоящие в разных позициях, имеют разныйвес. Так в целом десятичном числе 325 тройка означает три сотни, двойка – два десятка, пятерка - пять единиц: 325=3·100 + 2·10 +5·1. Такая запись называетсяразвернутой формой записи числа: число записывается в виде суммы, в которой каждое слагаемое – это цифра, умноженная на свой вес. Вот еще пример развернутой записи смешанного десятичного числа:
6248,547 = 6·1000 + 2·100 + 4·10 + 8·1 + 5·0,1 + 4·0,01 + 7·0,001= 6·103+ 2·102+ 4·101+ 8·100+ 5·10-1+ 4·10-2+ 7·1-3
В десятичной системе счисления веса равны степеням десятки (положительным и отрицательным). Каждая позиция в записи числа называетсяразрядом числа. Разряды нумеруются в целой части числа положительными целыми числами, начиная от нуля, в дробной части – отрицательными числами, начиная от минус единицы:
разряды: 3 2 1 0 -1-2-3
число: 6248,547
Здесь номера разрядов указаны маленькими цифрами сверху. Отсюда видно, что веса соответствующих цифр равны десяти в степени, равной номеру разряда, в котором стоит эта цифра.
Следующий, бесконечный в обе стороны ряд целых степеней десятки называетсябазисомдесятичной системы счисления:
… 109, 108, 107, 106, 105, 104, 103, 102, 101, 100, 10-1, 10-2, 10-3, …
Запись числа в развернутой форме еще называют разложением числа по базису.
Десятичная система относится к числутрадиционныхсистем счисления. Для традиционных систем счисления принято размерность алфавитаназывать основанием системы счисления. Основание десятичной системы счисления равно десяти.
По такому же принципу организованы все другие традиционные системы счисления. Наименьшим основанием для позиционной системы является 2 – двоичная система. Система с основание 1 не может быть позиционной, поскольку для нее невозможно построить базис - единица в любой степени равна единице. Базис двоичной системы счисления выглядит так:
… 29, 28, 27, 26, 25, 24, 23, 22, 21, 20, 2-1, 2-2, 2-3, …
Основанием традиционной позиционной системы может быть любое натуральное число, начиная от двух, а базис – бесконечный в обе стороны ряд целых степеней основания
Вот несколько примеров позиционных систем и их алфавитов:
| Основание | Название | Алфавит |
|---|---|---|
| Двоичная | 0 1 | |
| Троичная | 0 1 2 | |
| Восьмеричная | 0 1 2 3 4 5 6 7 | |
| Шестнадцатеричная | 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Еслиn– основание системы не большее десяти, то в алфавите используютсяnпервых арабских цифр. Если основание превышает 10, то в качестве дополнительных цифр выступают буквы латинского алфавита по порядку.
При записи недесятичного числа принято указывать его основание маленькой подстрочной цифрой – нижним индексом. Например: 1375– число в пятеричной системе счисления. Отметим одно очень важное обстоятельство:
в любой позиционной системе счисления ее основание записывается как 10.
Например: 102=2, 103=3, 108=8, 1016=16 и т.д.
Задача 1.Число в троичной системе счисления: 2011,13нужно перевести в десятичную систему.
Разложим данное число по базису троичной системы счисления, т.е. запишем его в развернутой форме и вычислим полученное выражение по правилам десятичной арифметики:
2011,13= 2·33+0·32+1·31+1·30+1·3-1=54+3+1+1/3=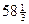
Задача 2. Шестнадцатеричное число 2AF,8C16перевести в десятичную систему.
Задача также решается через разложение шестнадцатеричного числа по базису системы счисления и вычисления полученного выражения. В разложении цифры, обозначаемые буквами, заменяются на их эквиваленты в десятичной системе.
2AF,8C16=2·162+10·16+15·160+8·16-1+12·16-2=512+160+15+1/2+3/64= 687,546875
Задача 3. Двоичное число 1010101111,1000112перевести в десятичную систему.
1010101111,1000112=1·29+1·27+1·25+1·23+1·22+1·2+1+1·2-1+1·2-5+1·2-6= 512 + 128 + 32 + 8 + 4 +2 + 1 +1/2 + 1/32 +1/64 =687,546875.
Обратите внимание, что результат тот же, что и в задаче 2. Значит двоичное число из данной задачи равно шестнадцатеричному числу из задачи 2. К этому обстоятельству мы еще вернемся.
Схема Горнера и перевод чисел
Недесятичное число можно быстро перевести в десятичную систему и с помощью простого калькулятора. Такой перевод связан с применением так называемойсхемы Горнерадля вычисления алгебраических многочленов. Сначала рассмотрим перевод целого числа на примере восьмеричного числа 2317458. Запишем его в развернутой форме и преобразуем полученную сумму к эквивалентной скобочной форме:
2317458= 2·85+3·84+1·83+7·82+4·8+5=((((2·8+3)·8+1)·8+7)·8+4)·8+5=78821
Раскройте мысленно скобки в записанном выражении, и вы увидите, что получится то же разложение по базису восьмеричной системы счисления. Но зато скобочное выражение очень просто вычислять. На калькуляторе нужно последовательно слева направо выполнять умножения и сложения. Порядок нажатия клавиш на калькуляторе будет таким:
| × | + | × | + | × | + | × | + | × | + | = | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
В калькуляторе реализуется алгоритм последовательного выполнения цепочки операций: при нажатии клавиши со знаком операции выполняется предыдущая операция и ее результат высвечивается на индикаторе. После нажатия клавиши «равно» выполняется последняя операция цепочки и на индикаторе отражается результат вычисления всего выражения. В рассмотренном примере было выполнено пять умножений и пять сложений. Такой способ вычисления называется схемой Горнера.
В общем виде алгебраический многочленn-й степени и его преобразование к скобочной форме выглядит так:

Из этой формулы следует, что алгебраический многочленn-й степени можно вычислит заnопераций умножения иnопераций сложения. Это самый оптимальный способ вычисления.
Схему Горнера можно применить и для перевода дробных чисел. Покажем на примере двоичного числа 0,1101012. Запишем число в развернутой форме и выполним тождественные преобразования, приводящие выражение к скобочной форме:
0,1101012= 1·2-1+1·2-2+0·2-3+1·2-4+0·2-5+1·2-6= 1·2-6+0·2-5+1·2-4+0·2-3+1·2-2+1·2-1=
=(((((1/2+0)/2+1)/2+0)/2+1)/2+1)/2= 0, 828125
Полученное выражение также поддается последовательному вычислению на калькуляторе: шесть операций деления и пять – сложения. Клавиши нажимаются в таком порядке:
| / | + | / | + | / | + | / | + | / | + | / | = | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Прибавление нулей можно не делать, тогда число операций сложения сократиться до трех:
| / | / | + | / | / | + | / | + | / | = | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Практическое задание №1
Выполните быстрый перевод в десятичную систему счисления следующих недесятичных чисел, пользуясь калькулятором и вычислительной схемой Горнера:
а) 32045, 11010112, 567218, 9A3CEF16;
б) 0,32045, 0,11010112, 0,567218, 0,9A3CEF16;